Elektronický vzdelávací materiál

Všeobecná rovnica priamky v rovine

Všeobecná rovnica priamky vychádza z poznatku, že priamka je v rovine jednoznačne určená bodom a normálovým vektorom.

Normálový vektor priamky p je každý smerový vektor priamky k kolmej na priamku p.

Pre každý bod X roviny platí, že bod X leží na priamke p práve vtedy, keď vektor s = AX = [x - a₁; y - a₂] je kolmý na smerový vektor priamky p, teda Potom:

X ∈ p ⇔ n ⊥ s

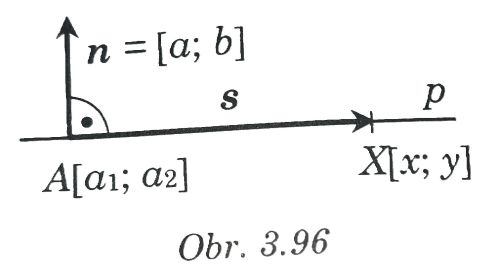
n * s = 0
a (x - a₁) + b(y - a₂) = 0
ax + by + (- aa₁ - ba₂) = 0

Rovnica ax + by + c = 0 kde a, b, c ∈ R a ≠ 0 b ≠ 0 , sa nazýva všeobecná rovnica priamky v rovine.